Population Growth- Logistic growth

The term ‘population growth’ refers to the change in the number of individuals in a population with time. It refers to how the number of individuals in a population increases or decreases with time.

Population growth- Introduction:

Population change is determined by four factors: birth, death, emigration, and immigration.
In a closed population, change in population is only related to birth and death of individuals.
In case of open population, birth, death, immigration and emigration result in a change of population.

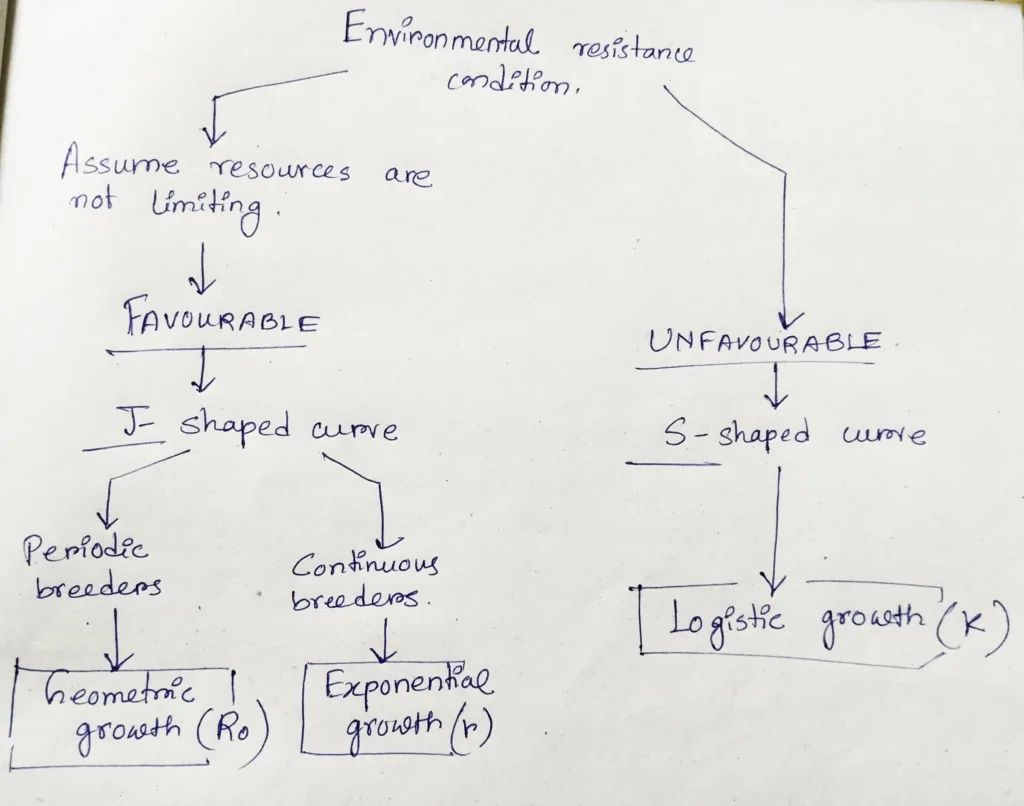
There are two types of environmental resistance conditions. One is favorable (unlimited resources) and the other one is unfavorable. Under favorable condition there are two types of growth- 1) geometric growth, 2) Exponential growth. Under unfavorable condition there is logistic growth.

Exponential Growth – explanation:

The exponential growth assumes that resources are unlimited, but it is never the case in the real life situation. As population density increases, each individual has access to fewer resources. It means a particular environment can only support a maximum population size.

The number of individuals of a particular species that a particular environment can support indefinitely is defined as carrying capacity (denoted by the letter K).

Carrying capacity is not fixed, but varies over space and the time with abundance of limited resources. It is determined by various factors including predation, competition and climate conditions. Since such factors are many and varied, itbis cleared that the carrying capacity of any area for a population may vary over a time period.

So, the growth of a population eventually slows as a population reaches the carrying capacity for environment. This is known as Verhulst-Pearl logistic growth.

The logistic model of population growth:

The logistic model of population growth produces a sigmoid (S-shaped) growth curve when population size is plotted over time. In sigmoid growth form, the population increases slowly at first (establishment or positive acceleration phase), then more rapidly (perhaps approaching a logarithmic phase), but it soon slows down eventually as the environmental resistance increases in percentage (the negative acceleration phase), until equilibrium is reached and maintained.

The upper level, beyond which no major increase can occur, as represented by the constant K, is the upper asymptote of the sigmoid curve and has been aptly called the carrying capacity.

We can modify the exponential equation to incorporate changes in growth rate near the carrying capacity. If the maximum sustainable population size i.e. carrying capacity is K, then K-N is the number of additional individuals the environment can accommodate, and (K-N) /K is the fraction of K that is still available for population growth.
By multiplying the exponential rate of increase r N by (K-N) /K, we can modify the growth rate of the population:

Where, N= population size; dN/dt= rate of change in population size; K = carrying capacity; r = intrinsic rate of increase.

The above equation for logistic growth was formulated by Francois Verhulst in 1838, which he called the logistic and having the differential form.

Other related notes:

1. Geometric growth: https://thebiologyislove.com/population-growth-geometric-growth/
2. Exponential growth: https://thebiologyislove.com/population-growth-exponential-growth/

Facebook link: https://www.facebook.com/share/p/Aukn9y4Kt5siKGCz/?mibextid=oFDknk

Instagram link: https://www.instagram.com/p/C79m7vOyaNB/?igsh=MTdiZDR3aWQzNTVlMw==