Doubling time

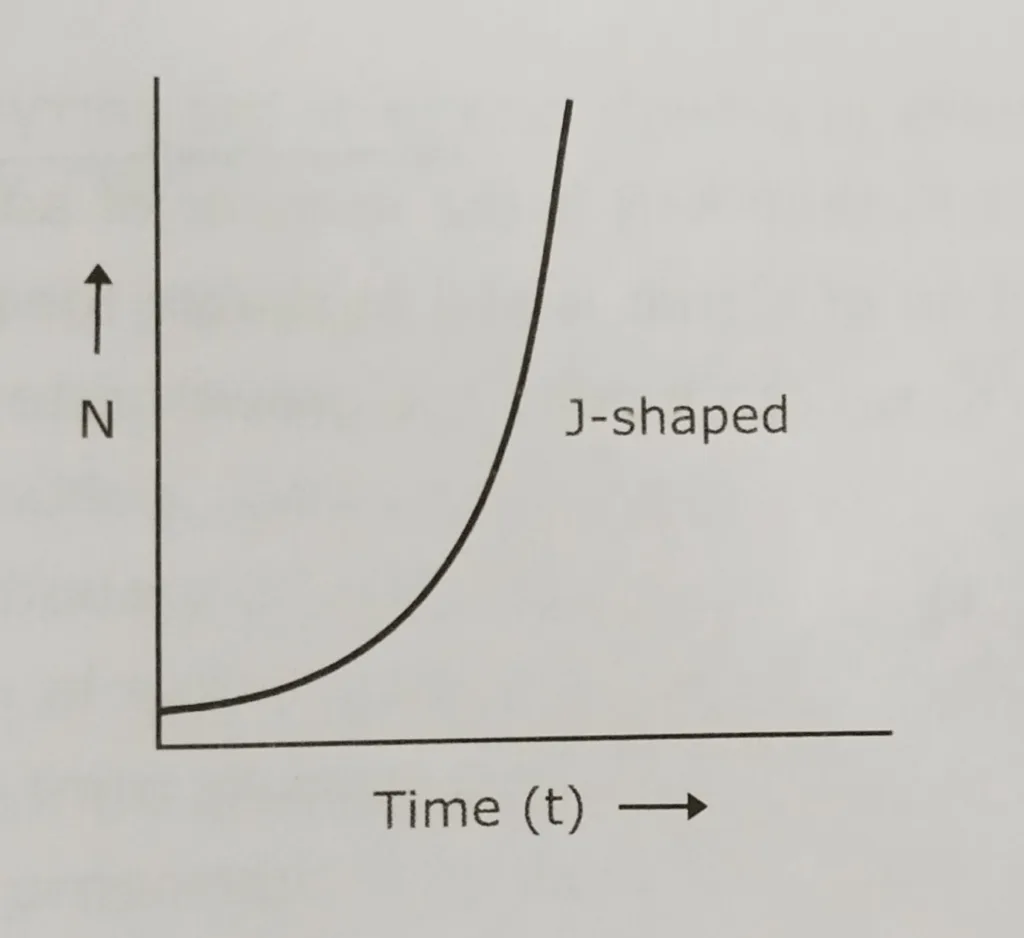
Doubling time (t_d) indicates how long the present population will take to double from its present or initial size. It is a measure of how rapidly a population grows.

Doubling time related to the equation of exponential growth

The t_d for an exponential function N₀e^rt is the time t_d (doubling time) that gives a population of 2 X N₀. Thus, we can get the doubling time by solving the equation:

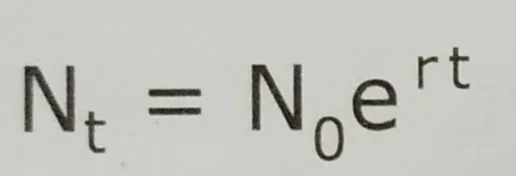
Deduction of the equation:

N_t = N₀e^rt

N_t= population density at time t
N₀= population density at time 0
r= intrinsic rate of natural increase

t= time interval
e= the base of the natural logarithm (constant about 2.7)
The term e to the power r is the factor by which the population increases during each time unit.

N_t = N₀e^rt

or, 2 X N₀ = N₀e^rt_d

or, e^rt_d = 2

[This equation indicates that rt_d is the power of e that gives 2.]

or, rt_d = ln 2

or, t_d = ln 2/r

Final formula for the calculation:

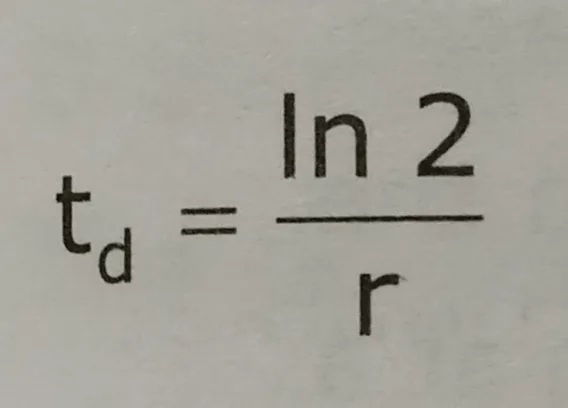
Where, t_d = Doubling time; r = intrinsic rate of increase

Conclusion:

From the above equation, if the intrinsic rate of increase (r) is easily known, the t_d of a population can be easily calculated. However, we assume that the population is not affected by its age distribution, and that r (the intrinsic rate of increase) is a constant during this period.

Other related link:

1. Population growth- Geometric growth: https://thebiologyislove.com/population-growth-geometric-growth/
2. Population growth- Exponential growth: https://thebiologyislove.com/population-growth-exponential-growth/

Facebook link: https://www.facebook.com/share/p/FpUSTdy4VfA9kyu5/?mibextid=oFDknk

Instagram link: https://www.instagram.com/p/C7d9ZVCxNGH/?igsh=enoxNXVkNnVlMjY0